그래프는 다양하게 있지만, 여기선 신장트리, 그 중에서도 MST (최소신장트리)에 대해 작성해보려고 한다. 신장트리 spanning tree: 그래프의 변형 트리는 부모 자식간의 관계, 그에 따른 차수, 높이가 있다. ex) 이진트리 여러 트리중에 신장트리란 각각의 정점들이 모두 연결된 트리 이다. 신장트리의 조건 (ST, spanning tree)(얘는 트리이므로)가중치는 있을 수 있지만, 무향(방향X)이다.cycleX () 그중에 최소신장트리(MST, minimum spanning tree)는 각각의 정점들이 최소비용으로 모두 연결되는 트리 이다.  MST 구현방법쿠르스칼 - 간선중심프림 - 정점 중심(간선이 많을 때 사용)MST - 쿠르스칼: 간선 기반 알고리즘으로 간선을 비용순으로 정렬하여 최소비..

최단경로가장 짧은 경로, 길찾기 최단경로 유형은 "한 지점에서 다른 지점까지의 최단경로",  "모든 지점에서 다른 모든 지점까지의 최단경로" 등으로 나눠볼 수 있다. 이러한 유형은다익스트라 알고리즘플로이드워셜 알고리즘그래프 알고리즘(BFS)greedy & DP 알고리즘벨만 포드 알고리즘등  정말 다양한 알고리즘으로 풀이할 수 있다. 다만 지금까지의 경험으로는 최단경로 문제는 왠만하면? 1~3번으로 거의 다 해결이 되는 느낌이었다.최단경로에는 가중치가 있는데 비용(cost), 거리(distance), 무게(weight) 이런식으로 있을 수 있다.  다익스트라현재 정점에서 다른 특정 정점가중치가 있는 경우O(NlogN) 플로이드워셜모든 정점에서 모든정점가중치가 있는 경우O(N^3) (ex) 사다리타기..?)..

[지금 무료] 스프링부트 개념정리(이론) 강의 | 최주호 - 인프런최주호 | 스프링부트를 공부하며 헷갈리는 개념이 많았던 분 스프링부트에 대해 공부하고 싶었던 모든 분, 스프링부트의 핵심은확실한 개념으로부터! 스프링부트 너무 어려운데 어떻게 시작하www.inflearn.comURECA 과정을 진행하면서 해당강의를 중심으로 스터디를 진행하고 있다. spring에 대해 1도 모르는 상태였기 때문에 개념정리를 목표로 시작했고, 현재 Spring과 JPA(1~7강)까지 정리한 상태이다. 복기를 위해 하나의 단원이 끝날 때마다 스터디 진행중에 논란?이 되었던 주제, 정확히 설명하지 못하는 주제에 대해 다시한번 정리하기로 했다. JPA : Entity 생명주기 관리영속성 컨텍스트를 통해 데이터 영구저장: 데이터를 ..

[지금 무료] 스프링부트 개념정리(이론) 강의 | 최주호 - 인프런최주호 | 스프링부트를 공부하며 헷갈리는 개념이 많았던 분 스프링부트에 대해 공부하고 싶었던 모든 분, 스프링부트의 핵심은확실한 개념으로부터! 스프링부트 너무 어려운데 어떻게 시작하www.inflearn.comURECA 과정을 진행하면서 해당강의를 중심으로 스터디를 진행하고 있다. spring에 대해 1도 모르는 상태였기 때문에 개념정리를 목표로 시작했고, 현재 Spring과 JPA(1~7강)까지 정리한 상태이다. 복기를 위해 하나의 단원이 끝날 때마다 스터디 진행중에 논란?이 되었던 주제, 정확히 설명하지 못하는 주제에 대해 다시한번 정리하기로 했다. JPA를 통해 Java로 데이터를 모델링 할 수 있음 ORM : 자바 필드 → DB 테..

[지금 무료] 스프링부트 개념정리(이론) 강의 | 최주호 - 인프런최주호 | 스프링부트를 공부하며 헷갈리는 개념이 많았던 분 스프링부트에 대해 공부하고 싶었던 모든 분, 스프링부트의 핵심은확실한 개념으로부터! 스프링부트 너무 어려운데 어떻게 시작하www.inflearn.comURECA 과정을 진행하면서 해당강의를 중심으로 스터디를 진행하고 있다. spring에 대해 1도 모르는 상태였기 때문에 개념정리를 목표로 시작했고, 현재 Spring과 JPA(1~7강)까지 정리한 상태이다. 복기를 위해 하나의 단원이 끝날 때마다 스터디 진행중에 논란?이 되었던 주제, 정확히 설명하지 못하는 주제에 대해 다시한번 정리하기로 했다. JPA : 자바를 통해 DB를 관리하기 위한 기술JPA = interfaceJPA(Ja..

정렬1. 선택 정렬: 가장 작은 데이터를 찾아서 순차적으로 앞쪽에 쌓는다선택 정렬의 특징첫번째 요소부터 나머지 요소들 중 가장 작은 요소와 자리를 교환한다.이 과정에서 앞에서부터 자동으로 정렬되게 된다.ex) 1회 : 9-1-7-5 -> 1-9-7-52회 : 1-9-7-5 -> 1-5-7-9// 선택 정렬 메소드 public static void selectionSort(int[] arr) { int n = arr.length; // 배열의 모든 요소를 순차적으로 탐색 for (int i = 0; i 선택 정렬의 시간 복잡도최악의 경우: O(n^2) 최선의 경우: O(n^2)평균: O(n^2) just 최악선택 정렬의 공간 복잡도O(1) (상수 공..

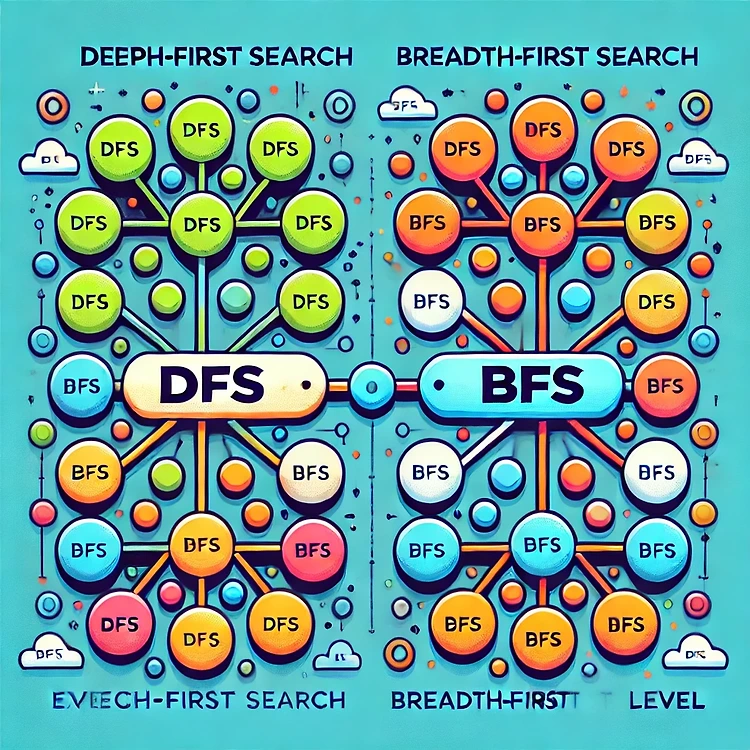
DFS, BFS그래프, tree를 어떻게 자료구조로 표현할것인가? 를 알기 위해 먼저 자료구조 Stack, Queue를 먼저 알아봤다.더보기 Java Platform SE 8 docs.oracle.comStack : FILO or LIFO 불공평한 자료구조 입구 1개 (입구와 출구가 같다)push(n) : n을 스택에 입력 / pop() : 맨 위(앞)에 있는 원소 반환 + 삭제 / peek() : 맨 위(앞)에 있는 원소 반환Stack의 자료구조는 stack, queue, arraydeque로 만들 수 있다. (하지만 왠만하면 arraydeque를 이용) Queue : FIFO 입구 1개, 출구 1개, 같은 방향으로 요소들이 흐른?다offer(n) : 큐 끝에 n 추가 / poll() : 큐 앞에 요소..

구현머릿속에 있는 알고리즘(사고)을 소스코드로 바꾸는 과정전형적인 문제풀이과정이 아닌, 문제를 읽고 이해해서 문제가 뭘 원하는지 파악해야한다. 문제가 요구하는 내용을 이해해서 이걸 코드로 작성(다양한 방법이 있음)시뮬레이션 : data 초기상태를 잘 받고, 규칙에 따를 수 있게 코드 작성 (시간의 흐름에 따라 데이터 수정등, 주로 반복문 사용)문제를 꼼꼼히 읽어야함 이것이 코딩테스트다 CH04. 예제1: n개의 방향을 입력받고, 방향에 따라 동서남북으로 이동 (단, 일정 범위를 넘어가는 방향은 무시), 최종적으로 도착한 좌표 출력더보기package 구현_ch04;import java.io.BufferedReader;import java.io.InputStreamReader;import java.util...

Greedy 탐욕법현재 상황에서 지금 당장 좋은 것만 고르는 방법개인적으로 알고리즘 방법중 가장 단순 무식한 방법, 단순 암기가 필요하지 않은 방법, 다양한 유형에서 어떻게든 답을 낼 수 있는 방법 이라고 생각한다. 모든 경우의 수를 다 따지는 완전 탐색(브루트포스)을 대비해서 꼭 필요한 (최선의) 선택을 통해서 답을 구함Greedy의 전제조건 : "수학적으로 증명된" 당연한 논리 (막연한 추측은 절대 네버 금물)타고난 수학적 직관력..(은 없어서) 오랜 경험을 통한 판단 해야한다.그래프 알고리즘(DFS, BFS) 에서 Greedy를 사용할 수 있다. 이것이 코딩테스트다 CH03.문제1 큰 수의 법칙: n개의 숫자들 중 m번 더해서 만들 수 있는 최대값을 출력 (단, 같은 수는 k번까지 반복 가능)더보기..

싱글톤 Singletonapplication을 통틀어 한 클래스에 대한 객체는 단 하나만 만드는 것.→ 때문에 new를 이용해서 객체를 생성하지 않는다. (클래스의 생성자가 private으로 설정되기 때문)→ 그렇다면? public 메소드를 만들어서(getInstance())이를 통해 객체를 생성하게 되는데 크게 3가지 방법이 있다. 1. 변수에 private 생성자에 new로 접근해서 객체를 먼저 넣고 returnprivate static Logger Logger = new Logger();- 이건 객체를 사용하기도 전에 미리 만드는 거라 객체가 클 경우 메모리 부담이 있음 2. 변수 선언만 하고 getInstance에서 객체 생성을 확인 후 생성   private static Logger Logger..